第36回企画展「地図で見るさいたまの近代」 展示Web解説 その1

第36回企画展「地図で見るさいたまの近代」 展示Web解説 その1

令和7年3月8日から6月1日まで開催した、第36回企画展「地図で見るさいたまの近代」 の展示内容を紹介します。

さいたま市域の姿は、江戸時代から様々な地図や絵図に描かれてきました。明治時代以降には、政府によって作られた地形図や、地租改正事業に伴って作られた土地の詳細な図面など、より正確な地図が作られるようになったほか、商業などの案内や広告、様々な事業に先立って作られる計画図など、目的に応じた多種多様な地図の中に描かれるようになりました。今回の企画展では、当館収蔵の地図を中心に展示し、近代の市域の姿やその変化のようすを紹介します。

地図の基礎知識

地図を作る目的やその使われ方は、江戸時代から現代に至るまで、それほど大きく変わってはいません。変化してきた点としては、様々な測量技術の発達により、精度が格段に高くなったことが挙げられます。
精度の高い地図を作ったり使ったりするときの重要な要素は「縮尺」（しゅくしゃく）と「方位」（ほうい）です。

縮尺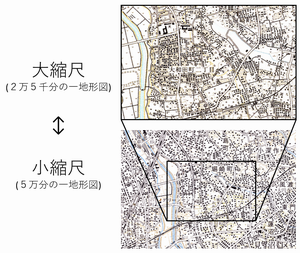

位置や方角を正確に表した地図は、現実の地面を一定の割合で縮小して紙の上に書き表します。この割合を「縮尺」といいます。近代では「5万分の1地形図」など分数で表すことが一般的ですが、江戸時代には「一分一間」（いちぶいっけん：紙面の1分（約3cm）が現実の1間（約1.8m）に相当）など、紙面と実際の長さを比較して表していました。分数で示す場合は、基本的に分子を1とするので、例えば地図上の1cmは、現実では分母の値（cm）となります。5万分の1の地形図では、地図上の1cmは現実の50,000cm＝500mにあたります。分母の数が大きくなるほど、同じ大きさの地図に入る現実の範囲の広さは大きくなります。分母が大きいほど分数の値としては小さくなるので「小縮尺」、逆に分母が小さく、現実の範囲が狭い地図は「大縮尺」の地図と呼ばれます。

方位

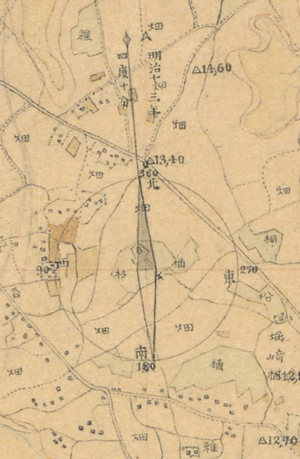縮尺と共に重要な要素が、地図上での東西南北がどちらになるかを示す「方位」です。北半球では、地図は北を上にして作られることが多く、その場合は表記が省略されていることもあります。北が上でない場合は、北がどの方向になるのかを描き表わすのが一般的です。地上で方位を知るためには方位磁石を使いますが、地球上では磁石が示す北の方角（磁北）と実際の地球の自転軸の位置（真北）がずれているため、両方の方角を示したり、両者のずれ（偏角）を角度で示したりすることで、地図を見る際に方角を正確に合わせられるようになっています。

さらに、地図の範囲が広くなると、地球の丸みをどのように平面に表すかを考える「図法」、「投影法」も重要になります。さいたま市域くらいの範囲の地図ではさほど問題になりませんが、地図の内容や目的に応じて様々な方法が考えられています。

まめちしき：尺貫法と地図の縮尺

江戸時代の地図は、上の縮尺のところで取り上げたように、地図上の一定の長さが現実のどのくらいの距離に対応するかで縮尺を表していました。江戸時代には、長さや距離を表すときには、尺貫法が使われていましたので、例えば「国絵図」のような小縮尺の地図では、地図上の6寸（約18cm）が現実の1里（約3.9km）となる縮尺、街道や宿場などの大縮尺の地図では、地図上の1分（約3mm）が現実の1間（約1.8m）になる縮尺などが使われていました。
近代になり、西洋、特にフランスから近代測量の技術を学んで地図が作られるようになると、長さや距離の表記についてもメートル法が取り入れられるようになりましたが、縮尺については江戸時代以来の、尺貫法できりのいい数字となるものも引き続き使われ続けました。このため、縮尺を分数で表した場合、一見して半端な数値になっている例がみられます。例えば上で挙げた「地図上の6寸が現実の1里」の縮尺は、分数で表すとおよそ「21,600分の1」、「地図上の1分が現実の1間」の縮尺はおよそ「600分の1」になります。今回展示している地図の中にも、これに似た「尺貫法ではきりのいい縮尺」の地図がありますので、ぜひ計算してみてください。

尺貫法での単位の比較

1里＝36町＝2,160間≒12,960尺＝129,600寸＝1,296,000分
1町＝60間≒360尺＝3,600寸＝36,000分
1間≒6尺＝60寸＝600分
※1間を何尺とするかについては、地域や時代によって6尺～6尺5寸ほどの間で差があります。

測量

地図を作るために、実際の土地やそこにある様々なものの形や位置を測り、紙の上に再現できるようにする作業が測量です。何を測るのかによっていろいろな方法がありますが、特に明治時代から昭和初期まで、地図を作るために良く使われた測量方法が「三角測量」と「水準測量」です。

三角測量

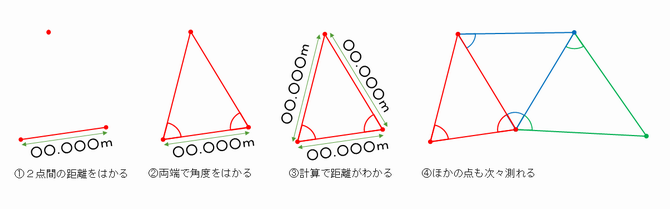
三角形は、ある1つの辺の長さと、その両端の頂点の角度を知ることができれば、形が定まり、他の2辺の長さやもう一つの頂点の角度も求めることができます。このことを利用して、まずどこかの2地点の間の距離を正確に測り、その2地点から、新たに距離を求めたい点への角度を測って三角形の形を定め、距離を求めるという測量の方法が「三角測量」です。遠く離れた山などでも、見通して角度を測ることができれば、計算で距離を求めることができるので、全国など広い範囲の地図を作るときに活用されました。頂点は何回も測量に使われるため、明治時代以降は強固な標識を設置しました。この標識は「三角点」と呼ばれます。

水準測量

地図上では地形の凹凸を直接表すことはできないため、等高線を描いたり、標高の値を記入したりすることで表します。この凹凸、つまり垂直方向の距離は、両方の点を見ることができる場所に、望遠鏡のような機器を水平に据え付け、両方の点に立てた定規の目盛りを読み取って、その差を計算して測ります。これが「水準測量」です。定規の長さ以上の高さの差がある場所や、同時に見通すことができない場所は、一度では測れないので、途中に仮の点を設け、機器を移動し、何回にも分けて測っていきます。
遠く離れた土地の高さの差を知りたいときに、毎回測りなおすのでは不便なため、既存の石造物に目印を取り付けたり、三角点のように標識を設置したりすることが行われました。この目印や標識は「水準点」と呼ばれます。

その2へ続く

次
その2 正確な地図(1)近代測量